Noteathon / LC-Top-Interview-Qs

LC-Top-Interview-Qs

July 29, 2021

LC-Top-Interview_Qs

Questions

Basic Tips

1. Two Sum

Solution

Approach 1: Brute Force - two loops check sum

Approach 2: Two_pass Hash Table : check for complement if not already present

Approach 3: One-pass Hash Table

It turns out we can do it in one-pass. While we are iterating and inserting elements into the hash table, we also look back to check if current element’s complement already exists in the hash table. If it exists, we have found a solution and return the indices immediately.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        prevMap = {}  # val -> index

        for i, n in enumerate(nums):
            diff = target - n
            if diff in prevMap:
                return [prevMap[diff], i]
            prevMap[n] = i

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i<nums.length;i++){
            // if the key is already present then gets, else inserts the current i
            int key = target - nums[i];
            
            if(map.containsKey(key)){
                // can return the answer in any order
                return new int[]{map.get(key), i};
            }
            
            
            map.put(nums[i],i);
        }
        return null;
    }
}

Complexity Analysis

Time complexity: O(n). We traverse the list containing n elements only once. Each lookup in the table costs only O(1) time.

Space complexity: O(n). The extra space required depends on the number of items stored in the hash table, which stores at most n elements.

2. Add Two Numbers

Solution
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        int carry = 0;
        ListNode dummy = new ListNode(-1);
        ListNode temp = dummy;
        while(l1!=null || l2!=null || carry!=0){
            int sum = 0;
            // Check if l1 list is not empty
            if(l1!=null){
                sum += l1.val;
                l1 = l1.next;
            }
            // Check if l2 list is not empty
            if(l2!=null){
                sum += l2.val;
                l2 = l2.next;
            }
            // Add previous carry if exists
            sum+=carry;
            temp.next = new ListNode(sum%10);
            temp = temp.next;
            // Current carry
            carry = sum/10;
        }
        // Return dummy Node next value
        return dummy.next;
    }
}

class Solution:
    def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
        carry = 0
        temp = ListNode() # default value is 0
        head = temp
        while l1 or l2 or carry: # check till any of the values are not zero or None
            sumIs = l1.val if l1 else 0
            sumIs += l2.val if l2 else 0
            sumIs += carry
            # print(sumIs)
            temp.next = ListNode(sumIs%10)
            carry = sumIs//10
            l1 = l1.next if l1 else None
            l2 = l2.next if l2 else None
            temp = temp.next
        return head.next

Complexity Analysis

Time complexity : O(max(m, n)). Assume that mm and nn represents the length of l1 and l2 respectively, the algorithm above iterates at most max(m, n) times.

Space complexity : O(max(m, n)). The length of the new list is at most max(m,n) + 1.

3. Longest Substring Without Repeating Characters

  • Find using the sliding window technique.
  • If the element is repeating then you move the other pointers
  • IMP : at any point both the pointers should move forward always.
Solution
class Solution {
    public int lengthOfLongestSubstring(String s) {
        int maxLen = 0;
        HashSet<Character> set = new HashSet<>();
        int j =0;
        for(int i=0; i<s.length();i++){
            //System.out.println("Hash Set : "+set +" i : "+i);
            char c = s.charAt(i);
            if(set.contains(c)){
                while(set.contains(c)){
                    //System.out.println("Removing : "+set);
                    set.remove(s.charAt(j++));
                }
            }
            
            set.add(s.charAt(i));
            maxLen = Math.max(maxLen, set.size());
            
        }
        return maxLen;
    }
}


/// ---- 2nd solution
public class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length(), ans = 0;
        Map<Character, Integer> map = new HashMap<>(); // current index of character
        // try to extend the range [i, j]
        for (int j = 0, i = 0; j < n; j++) {
            if (map.containsKey(s.charAt(j))) {
                i = Math.max(map.get(s.charAt(j)), i);
            }
            ans = Math.max(ans, j - i + 1);
            map.put(s.charAt(j), j + 1);
        }
        return ans;
    }
}

Complexity Analysis

TC : O(n), Index j will iterate n times. SC : O(min(m,n)). Same as the previous approach.

4. Median of two sorted arrays

Solution Video

  • Try to find the proper partition point. where Left < Right in both the parts.
  • Left is -INFINITY, Right -INFINITY
Solution
package com.interview.binarysearch;

/**
 * There are two sorted arrays nums1 and nums2 of size m and n respectively.
 * Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
 *
 * Solution
 * Take minimum size of two array. Possible number of partitions are from 0 to m in m size array.
 * Try every cut in binary search way. When you cut first array at i then you cut second array at (m + n + 1)/2 - i
 * Now try to find the i where a[i-1] <= b[j] and b[j-1] <= a[i]. So this i is partition around which lies the median.
 *
 * Time complexity is O(log(min(x,y))
 * Space complexity is O(1)
 *
 * https://leetcode.com/problems/median-of-two-sorted-arrays/
 * https://discuss.leetcode.com/topic/4996/share-my-o-log-min-m-n-solution-with-explanation/4
 */
public class MedianOfTwoSortedArrayOfDifferentLength {

    public double findMedianSortedArrays(int input1[], int input2[]) {
        //if input1 length is greater than switch them so that input1 is smaller than input2.
        if (input1.length > input2.length) {
            return findMedianSortedArrays(input2, input1);
        }
        int x = input1.length;
        int y = input2.length;

        int low = 0;
        int high = x;
        while (low <= high) {
            int partitionX = (low + high)/2;
            int partitionY = (x + y + 1)/2 - partitionX;

            //if partitionX is 0 it means nothing is there on left side. Use -INF for maxLeftX
            //if partitionX is length of input then there is nothing on right side. Use +INF for minRightX
            int maxLeftX = (partitionX == 0) ? Integer.MIN_VALUE : input1[partitionX - 1];
            int minRightX = (partitionX == x) ? Integer.MAX_VALUE : input1[partitionX];

            int maxLeftY = (partitionY == 0) ? Integer.MIN_VALUE : input2[partitionY - 1];
            int minRightY = (partitionY == y) ? Integer.MAX_VALUE : input2[partitionY];

            if (maxLeftX <= minRightY && maxLeftY <= minRightX) {
                //We have partitioned array at correct place
                // Now get max of left elements and min of right elements to get the median in case of even length combined array size
                // or get max of left for odd length combined array size.
                if ((x + y) % 2 == 0) {
                    return ((double)Math.max(maxLeftX, maxLeftY) + Math.min(minRightX, minRightY))/2;
                } else {
                    return (double)Math.max(maxLeftX, maxLeftY);
                }
            } else if (maxLeftX > minRightY) { //we are too far on right side for partitionX. Go on left side.
                high = partitionX - 1;
            } else { //we are too far on left side for partitionX. Go on right side.
                low = partitionX + 1;
            }
        }

        //Only we we can come here is if input arrays were not sorted. Throw in that scenario.
        throw new IllegalArgumentException();
    }

    public static void main(String[] args) {
        int[] x = {1, 3, 8, 9, 15};
        int[] y = {7, 11, 19, 21, 18, 25};

        MedianOfTwoSortedArrayOfDifferentLength mm = new MedianOfTwoSortedArrayOfDifferentLength();
        mm.findMedianSortedArrays(x, y);
    }
}

Complexity Analysis

Time complexity: O(log(min(m,n))).

Space complexity: O(1).

5. Longest Palindromic Substring

  • Brute Force approach will be O(n3), because we would be generating all substrings and then finding if it is palindrome.
  • e.g bab substrings, b,ba,bab,a,ab, so O(n2) substrings * O(n) for palindrome.
  • NOTE TODO : TBD dp solution. Solution Video
  • Try to expand from the centre, but remember there are two cases, odd even case so run the function twice.
Solution
class Solution {
    int maxLen = Integer.MIN_VALUE;
    String resSubstring = null;
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) return "";

        for(int i = 0;i<s.length();i++){
            //System.out.println(" Checking for char : "+s.charAt(i));
            // Odd case
            expandFromCentre(s, i, i);
            // Even case  : abbd, then check i and i+1
            expandFromCentre(s, i, i+1);
        }
        
        return resSubstring;
    }
    
    private void expandFromCentre(String s, int l, int r){
        // expand from the middle.
        while( l>=0 && r<s.length() && (s.charAt(l) == s.charAt(r))){
            int currLen = r - l + 1;
            if(currLen > maxLen){
                resSubstring = s.substring(l, r+1);
                maxLen = currLen;
            }
            l--;
            r++;
        }
    }
}

Complexity Analysis TC : O(n2), since we are running once, with i as the centre element of the string. SC : O(1) - constant for max string and len

7. Reverse Integer

  • 123 => 321 and alos -ve numbers.
  • Check the limits range [-2^31, 2^31 - 1].
  • Divide the MAX_NUM /10 and the current revNum to check if it is greater. If they are equal then compare with the last digit. Similary, for MIN_VALUE.
Solution
class Solution {
    public int reverse(int x) {
        int revNum = 0;
        while(x!=0){
            // Returns -ve for negative numbers
            int xMod = x % 10;
            // Removes the last number
            x = x/10;
            
            // reached positive limits
            if(revNum > Integer.MAX_VALUE/10 || ( revNum == Integer.MAX_VALUE/10 && xMod > 7)){
                return 0;
            }
            
            // reached negative limits
            if(revNum < Integer.MIN_VALUE/10 || ( revNum == Integer.MIN_VALUE/10 && xMod < -8)){
                return 0;
            }
            revNum = (revNum * 10) + xMod;
        }
        return revNum;
    }
}

Complexity Analysis TC : O(Log(n)) - Here the operation is running based on the number of digits, in the given number. So, the num of digits = Floor(Log10(n)). SC : O(1)

8. String to Integer (atoi)

  • This question is all about practiving limits and some string reading cases.
Solution
class Solution {
    public int myAtoi(String input) {
        int sign = 1; 
        int result = 0; 
        int index = 0;
        int n = input.length();
        
        // Discard all spaces from the beginning of the input string.
        while (index < n && input.charAt(index) == ' ') { 
            index++; 
        }
        
        // sign = +1, if it's positive number, otherwise sign = -1. 
        if (index < n && input.charAt(index) == '+') {
            sign = 1;
            index++;
        } else if (index < n && input.charAt(index) == '-') {
            sign = -1;
            index++;
        }
        
        // Traverse next digits of input and stop if it is not a digit
        while (index < n && Character.isDigit(input.charAt(index))) {
            int digit = input.charAt(index) - '0';

            // Check overflow and underflow conditions. 
            if ((result > Integer.MAX_VALUE / 10) || 
                (result == Integer.MAX_VALUE / 10 && digit > Integer.MAX_VALUE % 10)) {     
                // If integer overflowed return 2^31-1, otherwise if underflowed return -2^31.    
                return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
            }
            
            // Append current digit to the result.
            result = 10 * result + digit;
            index++;
        }
        
        // We have formed a valid number without any overflow/underflow.
        // Return it after multiplying it with its sign.
        return sign * result;
    }
}

Complexity Analysis TC : O(N), If N is the number of characters in the input string. We visit each character in the input at most once and for each character we spend a constant amount of time. SC : O(1) We have used only constant space to store the sign and the result.

11. Container With Most Water

Solution
  • Move towards the larger line by identifying the smaller line. So remove the smaller and move towards the larger line.
class Solution {
    public int maxArea(int[] height) {
        int l = 0;
        int r = height.length-1;
        int maxArea = Integer.MIN_VALUE;
        while(l<r){
            // the gap between the two lines
            int gap = r - l;
            int leftVal = height[l];
            int rightVal = height[r];
            int area = Math.min(leftVal, rightVal) * gap;
            maxArea = Math.max(area, maxArea);
            //System.out.println(" area : "+area +" l,r "+l+","+r);
            if(leftVal <= rightVal){
                l++;
            }else{
                r--;
            }
        }
        return maxArea;
    }                       
}

Complexity Analysis TC : O(n) - single pass SC : O(1) - constant

13. Roman to Integer

Solution
class Solution {
    HashMap<Character, Integer> map = new HashMap<>();
    public int romanToInt(String s) {
        map = new HashMap<>();
        map.put('I',1);
        map.put('V',5);
        map.put('X',10);
        map.put('L',50);
        map.put('C',100);
        map.put('D',500);
        map.put('M',1000);
        
        int sum = 0;
        for(int i=0;i<s.length();i++){
            // get current char val
            int curCharVal = map.get(s.charAt(i));
            Integer nextCharVal = null;
            // get next char value if present
            if(i+1<s.length()){
                nextCharVal = map.get(s.charAt(i+1));
            }
            
            // if next char exists
            if(nextCharVal!=null){
                // curr val is less then next then special cases
                if(curCharVal < nextCharVal){
                    sum+= nextCharVal - curCharVal;
                    i++;
                }else{
                    sum+= curCharVal;
                }
            }else{// if next doesnt exist then add to exisiting sum
                sum+=curCharVal;
            }
            //System.out.println(" i : "+i + ","+sum);
        }
        return sum;
    }
}

Complexity Analysis TC : O(1), since we are just lookup and using the values. Max is 3999 values which is constant SC : O(1), just 9 values in hashmap

14. Longest Common Prefix

Solution
class Solution {
    public String longestCommonPrefix(String[] strs) {
        // Take the first string
        String first = strs[0];
        int charPtr = 0;
        // for each charater in the first string
        while(charPtr < first.length()){
            for(int i=1;i<strs.length;i++){
                String str = strs[i];
                // if the character idx is > than the any of the strings, then return since it is out of bounds condition, may be we hit the smallest string.
                if(charPtr >= str.length() || str.charAt(charPtr) != first.charAt(charPtr)){
                    return first.substring(0,charPtr);
                }
            }
            // incerement if the character is present in all the strings.
            charPtr++;
        }
        return first.substring(0,charPtr);
    }
}

Complexity Analysis TC : O(nm) where n is the min of the m strings SC : O(1), not saving anything

15. 3Sum

Solution
class Solution {

    //2 pointers
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        LinkedList<List<Integer>> sol = new LinkedList<List<Integer>>();

        for (int i = 0; i < nums.length - 2; i++) {
            if (i == 0 || (i > 0 && nums[i] != nums[i - 1])) {
                int target = 0 - nums[i];
                int left = i + 1;
                int right = nums.length - 1;

                while (left < right) {
                    if (nums[left] + nums[right] == target) {
                        ArrayList<Integer> miniSol = new ArrayList<>();
                        miniSol.add(nums[i]);
                        miniSol.add(nums[left]);
                        miniSol.add(nums[right]);
                        sol.add(miniSol);
                        while (left < right && nums[left] == nums[left + 1]) {
                            left++;
                        }
                        while (left < right && nums[right] == nums[right - 1]) {
                            right--;
                        }
                        left++;
                        right--;
                    } else if (nums[left] + nums[right] > target) {
                        right--;
                    } else {
                        left++;
                    }
                }
            }
        }

        return sol;
    }
}

//HashSet
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Set<List<Integer>> res = new HashSet<>();

        Map<Integer, Integer> map = new HashMap<>();
        for(int i=0;i<nums.length;i++){
            map.put(nums[i], i);
        }

        // O(n2) two loops, contant time for hashmap look up.
        for(int i = 0;i<nums.length-2;i++){
            for(int j = i+1;j<nums.length-1;j++){
                int target = 0 - (nums[i] + nums[j]);
                // Search the target in map if exists.
                if(map.containsKey(target) && map.get(target) > j){
                    List<Integer> list = new ArrayList<>();
                    list.add(nums[i]);list.add(nums[j]);list.add(nums[map.get(target)]);
                    Collections.sort(list);
                    res.add(list);
                    }
                }
            }
        return new ArrayList<>(res);
    }
}

Complexity Analysis TC : O(n^2). twoSumII is O(n), and we call it n times. Sorting the array takes O(nlogn), so overall complexity is O(nlogn + n^2). ~~~ O(n2) SC : O(log N to N),depending on the implementation of the sorting algorithm. For the purpose of complexity analysis, we ignore the memory required for the output.

167. Two Sum II - Input Array Is Sorted

  • We know that the array is sorted, so the sum can be target and we can move pointers based on the target.
Solution
class Solution {
    public int[] twoSum(int[] nums, int target) {
        int start = 0; 
        int end = nums.length-1;
        
        while(start<end){
            int sum = nums[start] + nums[end];
            if(sum == target){
                return new int[]{start+1,end+1};
            }else if(sum > target){
                end--;
            }else{
                start++;
            }
        }
        // Incase no solution exists;
        return new int[]{-1,-1};
    }
}

Complexity Analysis TC : O(n). The input array is traversed at most once. Thus the time complexity is O(n). SC : O(1). We only use additional space to store two indices and the sum, so the space complexity is O(1).

17. Letter Combinations of a Phone Number

Solution
class Solution {
    public List<String> letterCombinations(String digits) {
        LinkedList<String> list = new LinkedList<>();
        // base case if length is 0 then return
        if(digits.length() == 0){return list;}
        
        // create map of return
        String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        // initial empty string
        list.add("");        
        for(int i = 0;i<digits.length();i++){
            while(list.peek().length() == i){
                // FIFO remove first
                String ans = list.remove();
                int digit = Character.getNumericValue(digits.charAt(i));
                // for each string add character; till the length is same
                for(char c : mapping[digit].toCharArray()){
                    list.add(ans +""+c);
                }
            }
        }
        // return the list of strings.
        return list;
    }
}

Complexity Analysis TC : O(4^N⋅N), where N is the length of digits. Note that 4 in this expression is referring to the maximum value length in the hash map, and not to the length of the input. The worst-case is where the input consists of only 7s and 9s. In that case, we have to explore 4 additional paths for every extra digit. Then, for each combination, it costs up to N to build the combination. This problem can be generalized to a scenario where numbers correspond with up to M digits, in which case the time complexity would be O(M^N⋅N). For the problem constraints, we’re given, M=4, because of digits 7 and 9 having 4 letters each. SC : O(1); since we are returning the result list.

19. Remove Nth Node From End of List

  • Brute force approach is by advancing and knowing the length and then based on that getting the node.
  • But using 1 - Pass, we maintain the gap between the two pointers and then delete.
Solution
public ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    ListNode first = dummy;
    ListNode second = dummy;
    // Advances first pointer so that the gap between first and second is n nodes apart
    for (int i = 1; i <= n + 1; i++) {
        first = first.next;
    }
    // Move first to the end, maintaining the gap
    while (first != null) {
        first = first.next;
        second = second.next;
    }
    second.next = second.next.next;
    return dummy.next;
}

Complexity Analysis TC : O(N) - n the length of the nodes SC : O(1)

20. Valid Parentheses

Solution
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        // Make mapping of the opening and closing brackets
        Map<Character, Character> map = new HashMap<>();
        map.put('(',')');
        map.put('{','}');
        map.put('[',']');
        
        // Check for each char if the closing bracking and opening match
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(map.containsKey(c)){
                stack.push(c);
            }else{
                if(!stack.isEmpty() && map.get(stack.peek()) == c){
                    stack.pop();
                }else{
                    return false;
                }
            }
        }
        // If all match then stack should be empty else false;
        return stack.isEmpty();
    }
}

Complexity Analysis TC : O(n) because we simply traverse the given string one character at a time and push and pop operations on a stack take O(1) time. SC : Space complexity : O(n) as we push all opening brackets onto the stack and in the worst case, we will end up pushing all the brackets onto the stack. e.g. ((((((((((.

21. Merge Two Sorted Lists

  • Check the optimization, if one the list becomes null after traversal then just point that to the pointer.
Solution
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        // maintain an unchanging reference to node ahead of the return node.
        ListNode prehead = new ListNode(-1);

        ListNode prev = prehead;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                prev.next = l1;
                l1 = l1.next;
            } else {
                prev.next = l2;
                l2 = l2.next;
            }
            prev = prev.next;
        }

        // At least one of l1 and l2 can still have nodes at this point, so connect
        // the non-null list to the end of the merged list.
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;
    }
}

Complexity Analysis TC : O(n+m) Because exactly one of l1 and l2 is incremented on each loop iteration, the while loop runs for a number of iterations equal to the sum of the lengths of the two lists. All other work is constant, so the overall complexity is linear SC : O(1) just point references.

22. Generate Parentheses

  • This is a backtacking question, where we remove the last character from the stack/string after adding all the open brackets.
Solution
class Solution {
    public List<String> generateParenthesis(int n) {
        List<String> ans = new ArrayList();
        backtrack(ans, new StringBuilder(), 0, 0, n);
        return ans;
    }

    public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max){
        if (cur.length() == max * 2) {
            ans.add(cur.toString());
            return;
        }

        if (open < max) {
            cur.append("(");
            backtrack(ans, cur, open+1, close, max);
            cur.deleteCharAt(cur.length() - 1);
        }
        if (close < open) {
            cur.append(")");
            backtrack(ans, cur, open, close+1, max);
            cur.deleteCharAt(cur.length() - 1);
        }
    }
}

Complexity Analysis Our complexity analysis rests on understanding how many elements there are in generateParenthesis(n). This analysis is outside the scope of this article, but it turns out this is the n-th Catalan number (1/n+1) (2n by n) which is 4n/n. sqrt n

TC : O(4n/sqrt n) Each valid sequence has at most n steps during the backtracking procedure. SC : O(4n/sqrt n), as described above, and using O(n) space to store the sequence.

23. Merge k Sorted Lists

  • There are 3 solutions using heap and merge solution.
  • All have a complexity of O(nLog(k))
Solution
//  Solution using Min Heap
//  Time Complexity:         O(n*log(k))
//  Extra Space Complexity:  O(k)

class Solution1 {
    public ListNode mergeKLists(ListNode[] lists) {
        Queue<Integer> minHeap = new PriorityQueue<>();

        for (ListNode nodes : lists) {
            ListNode current = nodes;
            while (current != null) {
                minHeap.add(current.val);
                current = current.next;
            }
        }

        ListNode dummy = new ListNode(0);
        ListNode current = dummy;

        while (!minHeap.isEmpty()) {
            current.next = new ListNode(minHeap.poll());
            current = current.next;
        }

        return dummy.next;
    }
}

//  Solution using Iterative Merge Sort
//  Time Complexity:         O(n*log(k))
//  Extra Space Complexity:  O(1)

class Solution2 {

    public ListNode mergeKLists(ListNode[] lists) {
        int size = lists.length;
        int interval = 1;

        while (interval < size) {
            for (int i = 0; i < size - interval; i += 2 * interval) {
                lists[i] = merge(lists[i], lists[i + interval]);
            }

            interval *= 2;
        }

        return size > 0 ? lists[0] : null;
    }

    private ListNode merge(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(0);
        ListNode curr = dummy;

        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                curr.next = l1;
                l1 = l1.next;
            } else {
                curr.next = l2;
                l2 = l2.next;
            }

            curr = curr.next;
        }

        if (l1 != null) {
            curr.next = l1;
        } else {
            curr.next = l2;
        }

        return dummy.next;
    }
}
// Solution using the Priority Queue with iterating heads.
class Solution3 {
    public ListNode mergeKLists(ListNode[] lists) {
        PriorityQueue<ListNode> pq = new PriorityQueue<>((o1,o2)->o1.val - o2.val);
        // Adding the heads of all the lists.
        for(ListNode node : lists){
            if(node!=null){
                pq.offer(node);
            }
        }
        ListNode temp = new ListNode(-1);
        ListNode res = temp;
        // Till the queue is not empty, remove the min head and then add back to the list.
        while(!pq.isEmpty()){
            ListNode head = pq.poll();
            if(head!=null){
                temp.next = new ListNode(head.val);
                temp = temp.next;
                if(head.next!=null){
                    // Moving the head forward and adding back to the heap
                    pq.offer(head.next);
                }
            }
        }
        // if the size of the list is empty then return the null node else the result node.
        return lists.length==0 ? null : res.next;
    }
}

Complexity Analysis TC : O(n*log(k)) where k are the linked list. Height of tree is log(K). N - nodes. SC : O(1)

26. Remove Duplicates from Sorted Array

  • Good solution by Stefan Pochmann

  • Code Explanation

    • The idea is to use two-pointers i and j.
    • Ptr i points to the old elements, and Ptr j running pointer.
    • Ptr i gets replaced if Ptr j finds a new element.
    • Time O(n), Space O(1)
Solution
class Solution {
    public int removeDuplicates(int[] nums) {
        int i = 0; 
        for(int j = 1;j<nums.length;j++){
            // If the two nums are equal then continue
            if(nums[i] ==  nums[j]){
                continue;
            }
            // if different then increment and store the new value
            nums[++i] = nums[j];
        }
        // return i + 1; after placing i unique elements.
        return i+1;
    }
}

Complexity Analysis TC : O(n) SC : O(1)

28. Implement strStr()

  • Not implemented using KMP
  • TODO : KMP has O(n+m) with space O(m)
Solution
// Solution 1
class Solution {
    public int strStr(String haystack, String needle) {
        for(int i = 0; i<haystack.length() - needle.length() + 1;i++){
            int j = 0;
            // if equal increment botht i and j
            while(j<needle.length() && haystack.charAt(i) == needle.charAt(j)){
                j++;
                i++;
            }
            // match found
            if(j == needle.length()){
                // return the last idx of i
                return i-=j;
            }else{
                // reset the progress
                i -= j;
                j = 0;
            }
        }
        // if no match found
        return -1;
    }
} 

// Solution 2
class Solution {
    public int strStr(String haystack, String needle) {
        return haystack.indexOf(needle);
    }
}

Complexity Analysis TC : O(n*m); SC : O(1)

29. Divide Two Integers

  • The TC is O(Log^2 n), can be reduced to O(Log n + Log n) if stored in a list, but has a tradeoff of space which is again storing doubles O(Log n)
  • Refer this Video for clear explanation
Solution
class Solution {
    public int divide(int dividend, int divisor) {

        // Special case: overflow.
        if (dividend == Integer.MIN_VALUE && divisor == -1) {
            return Integer.MAX_VALUE;
        }
        
        int isDividendNve = dividend < 0 ? -1 : 1;
        int isDivisorNve = divisor < 0 ? -1 : 1;
        
        
        dividend = Math.abs(dividend);
        divisor = Math.abs(divisor);
        
        int quo = 0;
        
        // Inital base case if atleast 1 is possible
        while(dividend - divisor >=0){
            int pow = 0;
            // if next multiple is gt > curr else we take just one
            while(dividend - (divisor<<1<<pow) >=0){
                pow++;
            }
            // Add atleast 1 possibility
            quo += 1<<pow;
            dividend -= divisor<<pow;
        }
        
        return quo * isDividendNve * isDivisorNve;
    }
}

Complexity Analysis TC : O(log n * log n) for searching and then halving and then searching SC : O(1)

36. Valid Sudoku

  • If brute force then 3 separate loops for row, col, box; which would 3*O(n2), but we can reduce by creating hashset with string.
  • NeetCode solution
Solution
class Solution {
    public boolean isValidSudoku(char[][] board) {
        HashSet<String> set = new HashSet<>();
        // Iterte through row and cols
        for(int row  = 0;row<9;row++){
            for(int col  = 0;col<9;col++){
                char c = board[row][col];
                // skip if it is a dot
                if(c=='.'){continue;}
                String rowVal = "r"+row+c;// R : 0 : Val
                String colVal = "c"+col+c;// C : 0 : Val
                int box = (row/3)*3 + (col/3);
                // Make total of 9 box for each 3*3 grid.
                String boxVal = "b"+box+c;// B : 0 : Val
                
                // check if cotains in set; else return false
                if(set.contains(rowVal) || 
                  set.contains(colVal) || 
                  set.contains(boxVal)){
                    return false;
                }
                
                // if unique then gets added
                set.add(rowVal);
                set.add(colVal);
                set.add(boxVal);
            }
        }
        
        return true;
    }
}

Complexity Analysis TC : O(n2) SC : 3 * O(n2) ~ O(n2); because worst case if it is correct sudoku with all the value filled.Row - O(n2) + Col - O(n2) + Box - O(n2),, so we will have around 243 values.

38. Count and Say

  • Iterative approach is to store the base case and then start from the 2.
Solution
class Solution {
    public String countAndSay(int n) {
        // If  n is 0 or less, return empty
        if(n <= 0){
            return "";
        }
        
        // if n 1 return base case
        String res = "1";
        if(n == 1){
            return res;
        }
        
        // if n > 1 then do
        for(int k=2;k<=n;k++){
            StringBuilder sb = new StringBuilder("");
            StringBuilder str = new StringBuilder(res);
            for(int i=0;i<str.length();i++){
                char curr = str.charAt(i);
                int count = 1;
                // count repeating and then append
                while(i+1<str.length() && ((str.charAt(i+1)) == curr)){
                    i++;
                    count++;
                }
                //System.out.println(" Count : "+count +" i,j "+i+","+j);
                sb.append(count+""+curr);
            }
            res = sb.toString();
        }
        return res;
    }
    
}

Complexity Analysis TC : O(k * n), where k is the length of the largest sequence till n. In this for each n, we iterate n times over the string generated every time. So, O (k*n) SC : O(1), where we append all the strings to builder.

49. Group Anagrams

  • There are two solutions.
  • Brute force is to sort each string and then store in the HashMap
  • Optimized is to count the freqeuence of each characters and then get the HashKey and store. The second method take the space O ( N . K. 26) ~ O(N.K)
Solution
// Solution 1 : O(N K log K)
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        if (strs.length == 0) return new ArrayList();
        Map<String, List> ans = new HashMap<String, List>();
        for (String s : strs) {
            char[] ca = s.toCharArray();
            Arrays.sort(ca);
            String key = String.valueOf(ca);
            if (!ans.containsKey(key)) ans.put(key, new ArrayList());
            ans.get(key).add(s);
        }
        return new ArrayList(ans.values());
    }
}

// Solution 2 : O( N . K )
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        if (strs.length == 0) return new ArrayList();
        Map<String, List> ans = new HashMap<String, List>();
        int[] count = new int[26];
        for (String s : strs) {
            Arrays.fill(count, 0);
            for (char c : s.toCharArray()) count[c - 'a']++;

            StringBuilder sb = new StringBuilder("");
            for (int i = 0; i < 26; i++) {
                sb.append('#');
                sb.append(count[i]);
            }
            String key = sb.toString();
            if (!ans.containsKey(key)) ans.put(key, new ArrayList());
            ans.get(key).add(s);
        }
        return new ArrayList(ans.values());
    }
}

Complexity Analysis TC : - Solution 1 : O(NKlogK), where N is the length of strs, and K is the maximum length of a string in strs. The outer loop has complexity O(N) as we iterate through each string. Then, we sort each string in O(KlogK) time. - Solution 2 : O(N.K.26), where N is the length of strs, and K is the maximum length of a string in strs. Counting each string is linear in the size of the string, and we count every string.

SC : O(NK), the total information content stored in ans.

48. Rotate Image

Solution
// Solution 1 using 4 places, top left, top right, btm left and right.
class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < (n + 1) / 2; i ++) {
            for (int j = 0; j < n / 2; j++) {
                int temp = matrix[n - 1 - j][i];
                matrix[n - 1 - j][i] = matrix[n - 1 - i][n - j - 1];
                matrix[n - 1 - i][n - j - 1] = matrix[j][n - 1 -i];
                matrix[j][n - 1 - i] = matrix[i][j];
                matrix[i][j] = temp;
            }
        }
    }
}

// Solution 2 
class Solution {
    public void rotate(int[][] matrix) {
        transpose(matrix);
        reflect(matrix);
    }
    
    public void transpose(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int tmp = matrix[j][i];
                matrix[j][i] = matrix[i][j];
                matrix[i][j] = tmp;
            }
        }
    }
    
    public void reflect(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) {
                int tmp = matrix[i][j];
                matrix[i][j] = matrix[i][n - j - 1];
                matrix[i][n - j - 1] = tmp;
            }
        }
    }
}

Complexity Analysis TC : Solution 1 : O(M) Let M be the number of cells in the matrix. O(M), as each cell is getting read once and written once. Solution 2 : O(M). We perform two steps; transposing the matrix, and then reversing each row. Transposing the matrix has a cost of O(M) because we’re moving the value of each cell once. Reversing each row also has a cost of O(M), because again we’re moving the value of each cell once. SC : O(1) because we do not use any other additional data structures.

46. Permutations

Solution
// Solution 1 :
class Solution {
  public void backtrack(int n,
                        ArrayList<Integer> nums,
                        List<List<Integer>> output,
                        int first) {
    // if all integers are used up
    if (first == n)
      output.add(new ArrayList<Integer>(nums));
    for (int i = first; i < n; i++) {
      // place i-th integer first 
      // in the current permutation
      Collections.swap(nums, first, i);
      // use next integers to complete the permutations
      backtrack(n, nums, output, first + 1);
      // backtrack
      Collections.swap(nums, first, i);
    }
  }

  public List<List<Integer>> permute(int[] nums) {
    // init output list
    List<List<Integer>> output = new LinkedList();

    // convert nums into list since the output is a list of lists
    ArrayList<Integer> nums_lst = new ArrayList<Integer>();
    for (int num : nums)
      nums_lst.add(num);

    int n = nums.length;
    backtrack(n, nums_lst, output, 0);
    return output;
  }
}

// Solution 2 :
public class Permutations {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        permute(nums, new boolean[nums.length], new ArrayList<>(), result);
        return result;
    }

    private void permute(int[] nums, boolean[] used, List<Integer> permutation, List<List<Integer>> result) {
        if (permutation.size() == nums.length) {
            result.add(new ArrayList<>(permutation));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) continue;

            used[i] = true;
            permutation.add(nums[i]);
            permute(nums, used, permutation, result);
            used[i] = false;
            permutation.remove(permutation.size() - 1);
        }
    }
}

Complexity Analysis TC : (Took from comments) First, I think the time complexity should be N x N!. Initially we have N choices, and in each choice we have (N - 1) choices, and so on. Notice that at the end when adding the list to the result list, it takes O(N). SC : Second, the space complexity should also be N x N! since we have N! solutions and each of them requires N space to store elements

50. Pow(x, n)

Solution
class Solution {
    public double myPow(double x, int n) {
        long N = n;
        if (N < 0) {
            x = 1 / x;
            N = -N;
        }
        double ans = 1;
        for (long i = 0; i < N; i++)
            ans = ans * x;
        return ans;
    }
}

// Solution 2 
class Solution {
    public double myPow(double x, int n) {
        long N = n;
        if (N < 0) {
            x = 1 / x;
            N = -N;
        }
        double ans = 1;
        double current_product = x;
        for (long i = N; i > 0; i /= 2) {
            if ((i % 2) == 1) {
                ans = ans * current_product;
            }
            current_product = current_product * current_product;
        }
        return ans;
    }
};

Complexity Analysis TC : // Solution 1 : O(n) times since we are multiplying it by N times // Solution 2 : Fast Power Algorithm Iterative O(logn). For each bit of n ‘s binary representation, we will at most multiply once. So the total time complexity is O(logn). SC :

53. Maximum Subarray

  • Brute force is calculating sum starting from each i till end, then comparing all the max values.

  • The idea is based on the previous (prefix Sum) and comparing the current number.

maxSubArray(A, i) = maxSubArray(A, i - 1) > 0 ? maxSubArray(A, i - 1) : 0 + A[i];
Solution
// SOlution 1 - Brute Force
class Solution {
    public int maxSubArray(int[] nums) {
       int max = nums[0];
        for(int i=0;i<nums.length;i++){
            int sum=0;
            for(int j=i;j<nums.length;j++){
                sum += nums[j];
                if(sum > max){
                    max=sum;
                }
                System.out.println(" Checked sum : "+sum+" , "+max +" i,j "+i+","+j);
            }
            System.out.println(" -- ");
        }
        return max;
    }
}

// Solution 2 Optimized DP
public int maxSubArray(int[] A) {
        int n = A.length;
        int[] dp = new int[n];//dp[i] means the maximum subarray ending with A[i];
        dp[0] = A[0];
        int max = dp[0];
        
        for(int i = 1; i < n; i++){
            dp[i] = A[i] + (dp[i - 1] > 0 ? dp[i - 1] : 0);
            max = Math.max(max, dp[i]);
        }
        
        return max;
}

Complexity Analysis TC : Sol 1 : O(n^2) and Solution 2 : O(n) SC : O(n) - dp array, not always required if we store the previous variable.

54. Spiral Matrix

  • Increase the top left bound and reduce the bottom right bound.
Solution
class Solution {
    public List<Integer> spiralOrder(int[][] result) {
        List<Integer> resultList = new ArrayList<>();
        int rowStart = 0;
        int colStart = 0;
        int rowLen = result.length-1;
        int colLen = result[0].length-1;
        while(rowStart <= rowLen && colStart <= colLen){
            // Right
            for(int j=colStart;j<=colLen;j++){
                //System.out.println("R i,j "+rowStart+","+j);
                resultList.add(result[rowStart][j]);
            }
            rowStart++;

            // Down
            for(int i=rowStart;i<=rowLen;i++){
                //System.out.println("D i,j "+i+","+colLen);
                resultList.add(result[i][colLen]);
            }
            colLen--;

            // Left
            for(int j=colLen;j>=colStart;j--){
                if(rowStart<=rowLen){
                    //System.out.println("L i,j "+rowLen+","+j);
                    resultList.add(result[rowLen][j]);
                }

            }
            rowLen--;

            //Up
            for(int i=rowLen;i>=rowStart;i--){
                if(colStart<=colLen){
                    //System.out.println("U i,j "+i+","+colStart);
                    resultList.add(result[i][colStart]);
                }
            }
            colStart++;
        }
        return resultList; 
    }
}

Complexity Analysis TC : O(M⋅N). This is because we visit each element once. SC : O(1). This is because we don’t use other data structures. Remember that we don’t include the output array in the space complexity.

55. Jump Game

Solution
// Solution 1 - Greedy approach O(n)
class Solution {

    public boolean canJump(int[] nums) {
        int goal = nums.length - 1;
        for (int i = nums.length - 2; i >= 0; i--) {
            if (nums[i] + i >= goal) {
                goal = i;
            }
        }
        return goal == 0;
    }
}

// Solution 2 Recursive O(n^2)
class Solution {
    int max;
    int[] dp;
    public boolean canJump(int[] nums) {
        max = 0;
        dp = new int[nums.length];
        Arrays.fill(dp,-1);
        helper(nums, 0);
        //System.out.println(" Dp : "+Arrays.toString(dp));
        return max == nums.length-1;
    }
    
    private int helper(int[] nums, int idx){
        
        //System.out.println("-");
        if(idx >= nums.length-1){
            return nums.length - 1;
        }
        
        if(dp[idx]!=-1){
            return dp[idx];
        }
        
        // cant go further
        if(nums[idx] == 0){
            return idx;
        }
        
        // i = 0;
        int choices = nums[idx];
        int limit = (idx+choices >= nums.length-1) ? nums.length-1 :idx+choices;
        for(int i = idx+1;i<=limit;i++){
            //System.out.println(" Check i : "+i +" M : "+max);
            int ret = helper(nums, i);
            max = Math.max(max,ret);
            dp[i] = max;
            if(max == nums.length-1){
                return max;
            }
        }
       
        
        return max;
    }
}

Complexity Analysis TC : Greedy - O(n). We are doing a single pass through the nums array, hence n steps, where n is the length of array nums. DP - O(n2) For every element in the array, say i, we are looking at the next nums[i] elements to its right aiming to find a GOOD or MAX index. nums[i] can be at most n is the length of array nums. SC : O(1) and DP - O(n). Recursion requires additional memory for the stack frames.

1010. Pairs of Songs With Total Durations Divisible by 60

  • This problem is similar to Two-Sum problem, but instead we search for the the reminder value.
  • The bruteforce approach is to calculat the sum at each point, and check if the mod 60 is 0.
  • The optimized approach is based on a simple intution, where we store the frequency of the reminder in the hashmap. 
    (x + y) % 60 == 0, which means that x%60 + y%60 == 60;
e.g. if x = 110; y = ?
110%60 + y = 60
y = 60 - 50;
y = 10;
So, in hash map we look the freq count of 10.
Solution

// Solution 1 : BruteForce, O(n^2)
class Solution {
    public int numPairsDivisibleBy60(int[] time) {
        int counter = 0;
        for(int i = 0;i<time.length-1;i++){
            for(int j = i+1;j<time.length;j++){
                if((time[i] + time[j]) % 60 == 0){
                    counter++;
                }
            }
        }
        return counter;
    }
}

// Approach 2 : O(n)
class Solution {
    public int numPairsDivisibleBy60(int[] time) {
        int counter[] = new int[60];
        int pairs = 0;
        for(int i = 0;i<time.length;i++){
            int mod = time[i] % 60;
            if(mod == 0){
                pairs+= counter[mod];
            }else{
                pairs+= counter[60 - mod];
            }
            counter[mod]++;
        }
        //System.out.println(" Time : "+ Arrays.toString(time));
        return pairs;
    }
}

Complexity Analysis TC : O(n), when n is the length of the input array, because we would visit each element in time once. SC : O(1), because the size of the array remainders is fixed with 60.

56. Merge Intervals

Solution
class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
        LinkedList<int[]> merged = new LinkedList<>();
        for (int[] interval : intervals) {
            // if the list of merged intervals is empty or if the current
            // interval does not overlap with the previous, simply append it.
            if (merged.isEmpty() || merged.getLast()[1] < interval[0]) {
                merged.add(interval);
            }
            // otherwise, there is overlap, so we merge the current and previous
            // intervals.
            else {
                merged.getLast()[1] = Math.max(merged.getLast()[1], interval[1]);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

Complexity Analysis TC : O(nlogn) Other than the sort invocation, we do a simple linear scan of the list, so the runtime is dominated by the O(nlogn) complexity of sorting. SC : O(logN) (or O(n)O(n)) If we can sort intervals in place, we do not need more than constant additional space, although the sorting itself takes O(log n) space. Otherwise, we must allocate linear space to store a copy of intervals and sort that.

66. Plus One

  • There is only 1 special case where all the input arr is 9 elements, so for that we have to create a new array and return.
  • Also remember, we dont have to carry the carry till the end, just the last number and the before one if it is 9.
Solution
class Solution {
  public int[] plusOne(int[] digits) {
    int n = digits.length;

    // move along the input array starting from the end
    for (int idx = n - 1; idx >= 0; --idx) {
      // set all the nines at the end of array to zeros
      if (digits[idx] == 9) {
        digits[idx] = 0;
      }
      // here we have the rightmost not-nine
      else {
        // increase this rightmost not-nine by 1
        digits[idx]++;
        // and the job is done
        return digits;
      }
    }
    // we're here because all the digits are nines
    digits = new int[n + 1];
    digits[0] = 1;
    return digits;
  }
}

Complexity Analysis TC : O(N) since it’s not more than one pass along the input list. SC : O(N) Although we perform the operation in-place (i.e. on the input list itself), in the worst scenario, we would need to allocate an intermediate space to hold the result, which contains the N+1 elements. Hence the overall space complexity of the algorithm is O(N).

69. Sqrt(x)

  • Remember, when the square check is out of bound use the Long keyword.
  • Brute Force is O(n)
  • Optimized is O(Logn)
Solution
// Solution 1 - Brute Force O(n)
class Solution {
    public int mySqrt(int x) {
        long i=0;
        while( (i * i) <= x){
            i++;
        }
        return (int) i-1;
    }
}

// Solution 2 - Binary search
class Solution {
  public int mySqrt(int x) {
    if (x < 2) return x;

    long num;
    int pivot, left = 2, right = x / 2;
    while (left <= right) {
      pivot = left + (right - left) / 2;
      num = (long)pivot * pivot;
      if (num > x) right = pivot - 1;
      else if (num < x) left = pivot + 1;
      else return pivot;
    }

    return right;
  }
}

Complexity Analysis TC : O(Log n), since it is getting divided by 2 everytime. SC : O(1)

70. Climbing Stairs

  • At each step, we have two choices either to take the step 1 or to take the step 2 : climbStairs(i,n)=(i+1,n) + climbStairs(i+2,n)
  • Brute force approach is recursiion without memoization, which would take O(2n).
  • After memoization, it would take O(n)
Solution
public class Solution {
    public int climbStairs(int n) {
        int memo[] = new int[n + 1];
        return climb_Stairs(0, n, memo);
    }
    public int climb_Stairs(int i, int n, int memo[]) {
        if (i > n) {
            return 0;
        }
        if (i == n) {
            return 1;
        }
        if (memo[i] > 0) {
            return memo[i];
        }   
        // sum of choice with 1 step and 2 steps.
        memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);
        return memo[i];
    }
}

Complexity Analysis TC : O(n) SC : O(n)

75. Sort Colors

Solution
// Solution 1 - Freq or Bucket sort way
class Solution {
    public void sortColors(int[] nums) {
        
        int[] freq = new int[3];
        
        // Calc freq of 0,1,2
        for(int i = 0;i<nums.length;i++){
            freq[nums[i]]++;
        }
        
        //System.out.println(" Array : "+ Arrays.toString(freq));
        
        // Replace the array items
        for(int i=0;i<nums.length;i++){
            
            if(freq[0] != 0){
                nums[i] = 0;
                freq[0]--;
            }else if(freq[1]!=0){
                nums[i] = 1;
                freq[1]--;
            }else{
                nums[i] = 2;
                freq[2]--;
            }
        }
    }
}

// Solution 2 - One Pass
class Solution {
    public void sortColors(int[] nums) {
        int left = 0;
        int right = nums.length-1;
        int k = left + 1;
        // 1 2 0
        while(k <= right){
            //System.out.println(" K : "+nums[k]);
            if(nums[k] == 0){
                swap(nums, left, k);
                // increment left after swap, since till that left part all are sorted or == 0 
                left++;
            }
            if(nums[k] == 2){
                swap(nums, right, k);
                // reduce right after swap, since till that right all are sorted or == 2
                right--;
                // Decrement and check again after swap
                k--;
            }
            k += 1;
        }
    }
    
    private void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

Complexity Analysis TC : O(N) since it’s one pass along the array of length N. SC : O(1) since it’s a constant space solution.

76. Minimum Window Substring

Solution
class Solution {
    public String minWindow(String s, String t) {
        
         if (s.length() == 0 || t.length() == 0) {
            return "";
        }
        
        // Make target freq count
        Map<Character, Integer> targetMap = new HashMap<>();
        Map<Character, Integer> windowMap = new HashMap<>();
        for(int i = 0;i<t.length();i++){
            char c = t.charAt(i);
            targetMap.put(c,targetMap.getOrDefault(c, 0)+1);
        }
        
        int start = 0;
        int end = 0;
        int required = targetMap.size();
        int formed = 0;
        int[] values = new int[]{-1,0,0};
        
        while(end<s.length()){
            
            char currChar = s.charAt(end);
            // Add to the window map
            windowMap.put(currChar, windowMap.getOrDefault(currChar, 0)+1);
            
            // Check if part of the target
            if(targetMap.containsKey(currChar)){
                // if count >= target then the character count is satisfied.
                Integer val1 = windowMap.get(currChar);
                Integer val2 = targetMap.get(currChar);
                
                // ****** VERY IMPORTANT else last test case wont pass
                // For more info : https://leetcode.com/problems/minimum-window-substring/discuss/266059/Why-you-failed-the-last-test-case%3A-An-interesting-bug-when-I-used-two-HashMaps-in-Java

                if(windowMap.get(currChar) - targetMap.get(currChar) == 0 ){
                    formed++;
                }
            }
            
            // Substring is formed, try reducing it, by incrementing left
            while(start <= end && formed == required){
                char startChar = s.charAt(start);
                // System.out.println(" Map : "+targetMap + windowMap);
                int subLen = end - start + 1;
                if(values[0] == -1 || subLen < values[0]){
                    values = new int[]{subLen, start, end};
                }
                
                //System.out.println(" "+s.substring(start,end+1));
                // Remove the start character
                
                windowMap.put(startChar, windowMap.get(startChar)-1);
                if(targetMap.containsKey(startChar) &&
                   windowMap.get(startChar) < targetMap.get(startChar)){
                    formed--;
                }
                start++;
            }
            end++;
        }
        // System.out.println(" Start , End "+start+","+end);
        if(values[0] == -1){
            return "";
        }
        String subString = s.substring(values[1], values[2]+1);
        return subString;
    }
    
}

Complexity Analysis TC : O(|S| + |T|) where |S| and |T| represent the lengths of strings S and T. In the worst case we might end up visiting every element of string S twice, once by left pointer and once by right pointer. |T| represents the length of string T. SC : O(∣S∣+∣T∣). |S| when the window size is equal to the entire string SS. |T| when T has all unique characters.

Solution
class Solution {
    boolean[][] visited;
    public boolean exist(char[][] board, String word) {
        
        visited = new boolean[board.length][board[0].length];
        
        // Check if the first character matches then call the helper
        for(int i = 0;i<board.length;i++){
            for(int j = 0;j<board[i].length;j++){
                if(board[i][j] == word.charAt(0)){
                    if(helper(i , j, 0, board, word)){
                        return true;
                    }
                }
            }
        }
        
        return false;
    }
    
    
    private boolean helper(int i,int j,int startIdx,char[][] board, String word){
        // if reached end then return true search completed
        if(startIdx == word.length()){
            return true;
        }
        
        // bounds check and the character similar to the next what we want
        if(i < 0 || i>=board.length || j<0 || j>=board[i].length || word.charAt(startIdx)!=board[i][j]
          || visited[i][j]){
            return false;
        }
        
        // add to visited arr
        visited[i][j] = true;
        if(helper(i+1,j,startIdx+1,board, word) ||
          helper(i-1,j,startIdx+1,board, word) ||
          helper(i,j-1,startIdx+1,board, word) ||
          helper(i,j+1,startIdx+1,board, word)){
            return true;
        }
        // remove after visit
        visited[i][j] = false;
        
        return false;
    }
}

Complexity Analysis TC :

  • O(N⋅3 ^ L ) where N is the number of cells in the board and L is the length of the word to be matched. For the backtracking function, initially we could have at most 4 directions to explore, but further the choices are reduced into 3 (since we won’t go back to where we come from). As a result, the execution trace after the first step could be visualized as a 3-ary tree, each of the branches represent a potential exploration in the corresponding direction. Therefore, in the worst case, the total number of invocation would be the number of nodes in a full 3-nary tree, which is about 3 ^L.
  • We iterate through the board for backtracking, i.e. there could be N times invocation for the backtracking function in the worst case. As a result, overall the time complexity of the algorithm would be O(N⋅3 L ). SC : The main consumption of the memory lies in the recursion call of the backtracking function. The maximum length of the call stack would be the length of the word. Therefore, the space complexity of the algorithm is O(L).

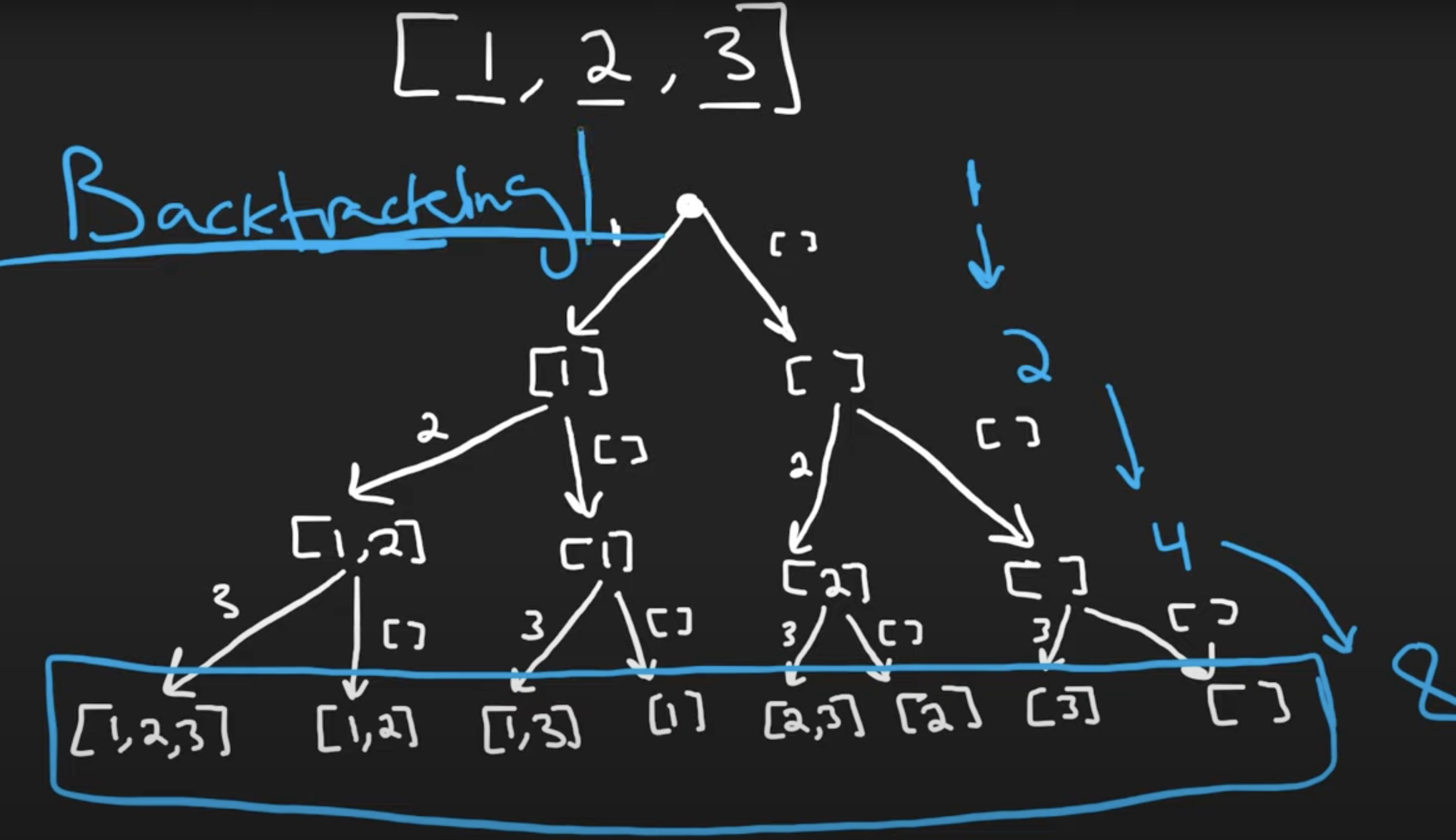
78. Subsets

Solution

class Solution {
    List<List<Integer>> result;
    public List<List<Integer>> subsets(int[] nums) {
        result = new ArrayList<>();
        backtrack(nums, 0, new ArrayList<>());
        return result;
    }
    
    
    private void backtrack(int[] nums, int idx, List<Integer> list){
        if(idx >= nums.length){
            // System.out.println(" List : "+list);
            result.add(new ArrayList<>(list));
            return;
        }
        
        // Add - Choice 1 - Includ
        list.add(nums[idx]);
        backtrack(nums, idx+1, new ArrayList<>(list));
        // Remove
        list.remove(list.size()-1);
        // Choice 2 - Dont Include
        backtrack(nums, idx+1, new ArrayList<>(list));
    }
}

// Solution 2 - Iterative Recursive
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        helper(0, nums, new ArrayList<>(), result);
        return result;
    }
    
    private void helper(int idx, int[] nums, List<Integer> list, List<List<Integer>> result){
        System.out.println(" List : "+list);
        // [], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3]
        // Choice 1 : Add the list as it is 
        result.add(new ArrayList<>(list));
        for(int i = idx;i<nums.length;i++){
            list.add(nums[i]);
            // Choice 2 : Add with the element and then remove
            helper(i+1, nums, list, result);
            list.remove(list.size()-1);
        }
    }
}

Complexity Analysis TC : O(N×2^N) to generate all subsets and then copy them into output list. We are going n levels, with each level having 2^n choices. SC : O(N). We are using O(N) space to maintain curr, and are modifying curr in-place with backtracking. Note that for space complexity analysis, we do not count space that is only used for the purpose of returning output, so the output array is ignored.

88. Merge Sorted Array

  • Brute force would be to merge both arrays using a new array and then use the sort function.
Solution
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int last = m + n - 1; // Equal to nums1.length - 1;
        // Compare the last elements which is m & n
        // This is better to do instead of taking m - 1 and n - 1, else bounds case to be written
        while(m > 0 && n > 0){
            if(nums1[m-1] > nums2[n-1]){
                nums1[last] = nums1[m-1];
                m-=1;
            }else{
                // lt equal then copy from nums2
                nums1[last] = nums2[n-1];
                n-=1;
            }
            last--;
        }
        
        // System.out.println("  m,n,last : "+m+","+n+","+last);
        // Remaining elements copy since they are already sorted
        // This means nums1 elems were less than nums2, else nums1 had pending.
        while(n>0){
            nums1[last] = nums2[n-1];
            last--;
            n--;
        }
    }
}

Complexity Analysis TC : O(n + m) since we are iterating both the arrays. SC : O(1) - just using constant variables.

91. Decode Ways

  • Two choices we have either to pick a single number or double number.
  • Increment the idx after you pick.
  • Check the iterative soltuion too.
  • Check Video
Solution


// Solution 1 : Recursive 
class Solution {
    int[] dp;
    public int numDecodings(String s) {
        dp = new int[102];
        Arrays.fill(dp, -1);
        return helper1(0,s);
    }
    
    private int helper1(int start, String s){
        
        if(dp[start] != -1){
            return dp[start];
        }
        
        if(start >= s.length()){
            return 1;
        }
        // If the start is 0 then it can't be decoded
        if(s.charAt(start) == '0'){
            return 0;
        }
        
        
        int firstNum = Integer.parseInt(s.substring(start, start+1));
        int secNum = 0;
        if(start+2<=s.length()){
            secNum = Integer.parseInt(s.substring(start, start+2));
        }
        
        //System.out.println(" Nums : "+firstNum + ", "+secNum);
        
        int ans = 0;
        // Check the choice 1, as it can be single number or double but not gt > 26
        if(firstNum>=1 && firstNum<=9){
            ans+=helper1(start+1, s);
        }
        // Check the choice 2, as it can be single number or double but not gt > 26
        if(secNum>=1 && secNum<=26){
            ans+=helper1(start+2, s);
        }
        
        return dp[start] = ans;
    }
}

Complexity Analysis TC : O(N), where N is length of the string. Memoization helps in pruning the recursion tree and hence decoding for an index only once. Thus this solution is linear time complexity. SC : O(N). The dictionary used for memoization would take the space equal to the length of the string. There would be an entry for each index value. The recursion stack would also be equal to the length of the string.

Word break

References

Next: Algorithms