Noteathon / Dynamic-Programming

Dynamic-Programming

July 6, 2022

Algorithms - My learning

Algorithms - My learning

Dynamic programming

DP is enhanced recursion (which calls 2 functions), where each functions inturn are overlapping. WHY 2 FUNCTIONS ? if it is skewed - - - then, no overlapping problems.
Another important thing is CHOICE, you would have choice in choosing the function.
Next is getting the optimal output.
How to identify a DP problem ?
- Check if there is choice (whether you want to put in knapsack or not)
- Check whether you have to find optimal (get max profit)
Bottom Up vs Top-Down
- Stack : Excessive recursive calls may lead to the stack overflow error, which would be avoided in the bottom up solution case. But this happens rarely (e.g. Scrambled String which comes under MCM topic)

1. Knapsack - 0|1

Fractional Knapsack (Greedy) : When you can fill the bag by using the fraction of the item
0/1 : So item as a whole (1) or nothing (0). Supply is only 1.
Unbounded Knapsack : When the supply is unlimited, you can keep putting till the limit is reached. Multiple occurrence of same item are allowed.
Here there are two properties for each item (Not that all problems have these properties, some might have just weight)
- Value which would sum for profit
- Weight
Clue to identify knapsack : given items, choice to whether include or not an item; and getting the max weight.

1.1 0-1 Knapsack
- Google Docs Code
  - Top Down Code
  - Bottom up approach
1.2 Subset Sum
- Question here is given the arr : {2,3,7,8,10}, check whether the sum of 11 is possible or not ?
- When compared to the previous problem, the Weight arr is not given, so we can omit it.
- Next observation is the Max Values, instead of max value it is Possible Subset. So, Max of numbers replace with True or False.
- Bottom Up code
1.3 Equal Sum
- Question here is give the arr : {1,5,5,11}, check whether the two subset exists with sum 11. In this it exists, Sub1{1,5,5} and Sub2{11}
- Pattern the core logic : Odd/Even. If the sum of the whole subset is 22 then only you can divide and create two partitions. If the sum was 23, then in no way you can divide the sum.
- To find the Subset Sum exists, just have to check the half the sum, because the other half would be present in the array anyways.
- Pseudo Code
```
 if isEven(arr_sum)
      return (SubsetSum(sumOfArr/2))
  else
      return false
```
1.4 Count of Subset Sum
1.5 Min subset sum diff
1.6 Target Sum
1.7 No of subset given diff

2. Knapsack - Unbounded

In an unbounded knapsack, the items in the value reduce only if they are processed, else they can be added again to the sack.

2.1 Unbounded Knapsack
2.2 Rod Cutting
2.3 Coin Change I
2.4 Coin Change II
2.5 Maximum Ribbon Cut

3. LCS

There are total of 14 problems. Palindrome questions are subset of LCS. Try to do the pattern matching in identifying the questions based on the Question similarity, Inputs and outputs. Check if they are asking optimal anything in terms of quantitative.

3.1 Longest common Subsequence

Recursive

    /* Returns length of LCS for X[0..m-1], Y[0..n-1] */
    int lcs(char[] X, char[] Y, int m, int n)
    {
        if (m == 0 || n == 0)
            return 0;
        if (X[m - 1] == Y[n - 1])
            return 1 + lcs(X, Y, m - 1, n - 1);
        else
            return max(lcs(X, Y, m, n - 1), lcs(X, Y, m - 1, n));
    }

Bottom Up

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
    int lcs(char[] X, char[] Y, int m, int n)
    {
        int L[][] = new int[m + 1][n + 1];

        /* Following steps build L[m+1][n+1] in bottom up fashion. Note
        that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */
        for (int i = 0; i <= m; i++) {
            for (int j = 0; j <= n; j++) {
                if (i == 0 || j == 0)
                    L[i][j] = 0;
                else if (X[i - 1] == Y[j - 1])
                    L[i][j] = L[i - 1][j - 1] + 1;
                else
                    L[i][j] = max(L[i - 1][j], L[i][j - 1]);
            }
        }
        return L[m][n];
    }

3.2 Longest common Substring

Check thread on Leetcode

Similar to Longest Common Subsequence LCS :
If characters are equal : dp[i][j]=1 + dp[i-1][j-1]
else dp[i][j]=0 // this is the only change

    public int  lgstComnSubstrDP(String str1, String str2){
        int m = str1.length();
        int n = str2.length();
        int maxLen = 0;
        int[][] dp = new int[m+1][n+1];

        for(int i = 0; i<=m; i++){
            for(int j = 0; j<=n; j++){
                if(i == 0 || j == 0)
                    dp[i][j] = 0;
                else if(str1.charAt(i-1) == str2.charAt(j-1))
                    dp[i][j] = 1+dp[i-1][j-1];
                else
                    dp[i][j] = 0;
                maxLen= Math.max(dp[i][j], maxLen);
            }
        }

        return maxLen;
    }

3.3 Printing LC Subsequence and String

To print it, you should observe the dp matrix that is generated. As, shown int the below image, we are following a pattern.

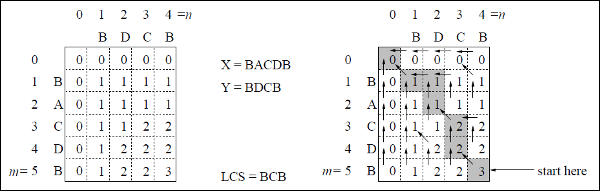
Algorithm

  if weights_equal
      add_char_to_word()
  else
      move_towards_directionOf_Max(top, left)

Implementation

  string ans;
  int i = m, j = n;
  while(i > 0 && j > 0)
  {
      // If current character in both the strings are same, then current character is part of LCS
      if(str1[i - 1] == str2[j - 1])
      {
          ans.push_back(str1[i-1]);
          i--;
          j--;
      }
      // If current character in X and Y are different & we are moving leftwards
      else if(dp[i - 1][j] > dp[i][j - 1])
      {
          j--;
      }
      // If current character in X and Y are different & we are moving upwards
      else
      {
          i--;
      }
        
  }
  reverse(ans.begin(), ans.end());

3.4 Shortest common supersequence

Part_1 : Shortest common SuperSequence

Leetcode
Length of the shortest supersequence = (Sum of lengths of given two strings) - (Length of LCS of two given strings)

Part_2: Print Shortest common SuperSequence

Just traversal towards the MAX dp element direction till one of the idx reaches 0.
LeetCode

        // Traverse from the back the dp array
        while(i>0 && j>0){
            if(str1.charAt(i-1) == str2.charAt(j-1)){
                // Move diagonally
            }else{
                if(dp[i][j-1] > dp[i-1][j]){
                    // Move left and that block char
                }else{
                    // Move top and that block char
                }
            }
        }
        
        // If remaining up direction
        while(i>0){
            sb.append(str1.charAt(i-1));
            i--;
        }
        // If remaining left direction
        while(j>0){
            sb.append(str2.charAt(j-1));
            j--;
        }
        return sb.reverse().toString();
    }

3.5 Min no of insertion and deletion a->b

Leetcode
Algorithm:
- str1 and str2 be the given strings.
- m and n be their lengths respectively.
- len be the length of the longest common subsequence of str1 and str2
- minimum number of deletions minDel = m – len
- minimum number of Insertions minInsert = n – len
- Note : Similar Question to be checked.

3.6 Longest palindromic subsequence

Leetcode
In this question inputs dont match, there might be chance that the secons string should be hidden or a function,derivative of the first string or redundant.
Here, the second string is redundant, since to find the Longest Palindromic SubSequence (LPS) of a, we just need to compare it with the reverse of the string and find the longest LCS.

    LPS(a) = LCS(a, reverse(a));

3.7 Min no of deletions in string to make it palindrome

Leetcode
To make the min nuumber of deletions, you have to create the longest palindromic subsequence. Min is inversely proportion to Longest.

    MinDel = totalLen - LPS(a)

3.8 Longest Repeating subsequence

LeetCode

    if(X[i-1]==Y[j-1] && i!=j) { // this is the only extra condition
        dp[i][j]=1+dp[i-1][j-1];
    }                

3.9 Sequence Pattern matching

- The idea is simple, to find the LCS and the LCS should be the string itself. The range of LCS can be from **0 to minLen(a,b)**.

    isLen( LCS(a,b)) == minLen(a,b);

3.10 Min no of insertions in string to make it palindrome

- The idea is similar to **Min number of deletion to make it LPS**.
- So we either add or delete to make it palindrome.

3.11 Note - TBD:

- Length of largest subsequence of 'a' which is substring in 'b'
- Subsequence pattern and matching
- Count how many times 'a' appears as subsequence in 'b'
- Largest palindromic substring
- Count of palindromic substring

4. Matrix chain multiplication (MCM)

Read this LeetCode_Post.
Pattern : The problem is not about the computation, rather the order to be performed in so as to get the optimal answer.
E.g based on associate law it is okay to perform multiplication in any way as shown below. But the cost involved in the performing operations is what makes it different. (ABC)D = (AB)(CD) = A(BCD)

4.1 MCM base

Problem statement explained on GeekForGeeks
Identification MCM is based on input either String, Array,where we have to find optimal somethings using partitions or either iterating the whole string.

// "static void main" must be defined in a public class.
public class MCM {
    static int[][] dp;
    public static void main(String[] args) {
        MCM obj = new MCM();
        System.out.println("Hello World!");
        int[] arr = {40,20,30,10,30};
        // dp initialization
        dp = new int[arr.length][arr.length];
        for(int[] row : dp){
            Arrays.fill(row,-1);
        }
        int value = obj.solve(arr,1,arr.length-1);
        System.out.println(" Value : "+value);
        for(int i = 0;i<arr.length;i++){
            for(int j = 0;j<arr.length;j++){
                System.out.print(dp[i][j]+",");
            }
            System.out.println();
        }
    }
    
    public int solve(int[] arr, int i, int j){
        int minValue = Integer.MAX_VALUE -1;
        if(i>=j){//if equal then only 1 element; so included equal too
            return 0;
        }
        
        // Memoization to store the min value in the i-j range from all the possible subsets.
        if(dp[i][j]!=-1){
            return dp[i][j];
        }
        
        for(int k=i;k<j;k++){ // Runs tilll j-1
            int ans = solve(arr,i,k) + solve(arr,k+1,j) + (arr[i-1] * arr[k] * arr[j]);
            System.out.println(" Sub Value : "+ans +" Range value : "+i+","+k+","+j);
            dp[i][j] = minValue = Math.min(ans, minValue);
        }
        return minValue;
    }
}

When memoized the value it stores the min value in the range.
M (Col:2 - Row:4) indicates the min value range. To know more, see below
- Based on the arr = {40,20,30,10,30}
  - M₁ : 40 * 20
  - M₂ : 20 * 30
  - M₃ : 30 * 10
  - M₄ : 10 * 30
- M₂.(M₃.M₄) = 6000 + 9000 = 15000
- (M₂.M₃).M₄ = 6000 + 6000 = 12000
- Since, Min(12000,15000) = 12000; the value M_2..4 will be equal to 12000.

Matrix Range	0	1	2	3	4
0	-1	-1	-1	-1	-1
1	-1	-1	24000	14000	26000
2	-1	-1	-1	6000	12000
3	-1	-1	-1	-1	9000
4	-1	-1	-1	-1	-1

4.2 Evaluate expression to TRUE/Boolean parenthization

Hey! Crazy question . GFG : Boolean Parenthesization Problem . The idea is to find the way that the expression is evaluate to TRUE.
e.g. expr : T|F&T^F has 5 ways listed below
1. ( T|F ) & ( T^F )
2. T | ( ( F&T )^F )
3. T | ( F& ( T^F ) )
4. ( ( T|F ) & T ) ^ F
5. ( T | ( F&T ) )^F

How to know whether the expression is True or False;

expr ` T F` has a leftTrue : 1 and rightFalse : 1

For each operator ‘ | ‘, we have calculation based on the truth table.

p	q	p OR q
T	T	T
T	F	T
F	T	T
F	F	F

Here to know the no of True values, we have to add the sum
- TrueValue = (leftTrightF) + (leftFrightT) + (leftT*rightT);
- FalseValue = (leftF*rightF)
Because of the above case, at every point to evaluate an expression we need to know to left and right values. In addition to that we also need to check whether it is True ‘T’ or False ‘F’ based on the character and boolean that we are checking case whether true or false.
- if istrue==1 & str[i] ='T' it means we required a true and got it so return 1 else return 0
- if istrue==0 & str[i] ='F' it means we required a false and got it so return 1 else return 0
Memoization, unlike other dp we are also isTrue/False, so need to track 3 variables. Can store in a Map( i +" "+j+" "+isTrue) or 3D Matrix dp = new int[str.length()+1][str.length()+1][2];

    int solve(String str, int i, int j, int istrue)
    {
        if(i>j)return 0;
        if(i==j)
        {  
		     // if istrue==1 & str[i] ='T' it means we required a true and got it so return 1 else return 0
			 // if istrue==0 & str[i] ='F' it means we required a false and got it so return 1 else return 0
			 
            if(istrue == 1)return (str.charAt(i)=='T')?1:0;   
            else return (str.charAt(i)=='F')?1:0;
        }     
        int ans=0;
        // dp checking value. Use 3d matrix or map for better vizualization
        if(dp[i][j][istrue]!=-1){
            return dp[i][j][istrue];
        }
        // parition at the logical operator, so that you have the left subpart and the right subpart.
        for(int k=i+1;k<=j-1;k=k+2)
        {
            // Get left T,F and right T,F so that you can know how true exists, which will help in summing up the number of true values.
            int leftT=  solve(str,i,k-1,1);
            int leftF=  solve(str,i,k-1,0);
            int rightT= solve(str,k+1,j,1);
            int rightF= solve(str,k+1,j,0);

            if(str.charAt(k)=='^')
            {
                if(istrue == 1)
                ans+=(leftT*rightF) + (leftF*rightT);
                else ans+=(leftT*rightT) + (leftF*rightF) ;
            }
            else if(str.charAt(k)=='&')
            {
                if(istrue == 1)
                ans+=(leftT*rightT);
                else ans+=(leftT*rightF) + (leftF*rightT) + (leftF*rightF);
            }
            else if(str.charAt(k)=='|')
            {
                if(istrue == 1)
                ans+=(leftT*rightF) + (leftF*rightT) + (leftT*rightT);
                else ans+=(leftF*rightF) ;
            }
            
            System.out.println("Char : "+str.charAt(k)  +" Ans :  "+ans+" L " + " : " +  leftT + ", " +  leftF + ", R : " +  rightT + ", " +  rightF +" Substring : "+str.substring(i,j+1) + " " + (istrue == 1));
        }
        return dp[i][j][istrue] = ans;    }

4.3 Palindrome partitioning

Worst case partitions will be : len(str) - 1
if string isEmpty or palindrome then 0 partition required
Identify keywords : min partition, left-right traversal.
The test cases fails without the Left Part optimization, since at any point to be the cuts optimized the left parts all should be optimized. So, since before checking right, we are also checking if the left part is optimized. e.g. abbd we will check, a > bb then d
Leetcode Problem : Palindrome Partitioning II

LeetCode solution

  int solve(String str, int i, int j){
      //Base Cases
      if(i>=j){
          return 0;
      }
      if(dp[i][j]!=null){
          return dp[i][j];
      }
        
        
      /*If the current string is palindrome then we dont need to break it into 
      further sub problems as we want to minimize the cuts.*/
      if(isPalindrome(str, i, j)){
          dp[i][j]=0;
          return 0;
      }
        
        
      int min = Integer.MAX_VALUE;
      //Trying Different possible cuts between i and j
      for(int k = i; k<=j;k++){
            
          /*An Optimization: We will make the partition only if the string till the partition 
          (till Kth position) is a valid palindrome. Because the question states that all 
          partition must be a valid palindrome. If we dont check this, we will have to 
          perform recursion on the left subproblem too (solve(str, i, k)) and	we will waste 
          a lot of time on subproblems that is not required. Without this the code will give
          correct answer but TLE on big test cases. */
          if(isPalindrome(str, i, k)){
              int partitions = 1+solve(str, k+1, j);
              min = Math.min(min, partitions);                
          }
            
            
      }
        
      //Store answer in the memo table
      dp[i][j]=min;
      return dp[i][j];
  }

4.4 Egg dropping problem

More resources or detaliled explanation Pepcoding, AlgoTree, BackToBackSWE
Leetcode : Super Egg drop problem
Check for optimization on how to convert to a binary search problem on Youtube
Check different solutions, they way they are optimized.

    public int superEggDrop(int e, int f) {
        // k eggs and n floors
        // if the floor is 1, then check only once, if no true floor then return
        if(f == 1 || f==0){
            return f;
        }
        
        // if you have 1 egg, then you have to test at each floor.
        if(e == 1){
            return f;
        }
        
        if(dp[e][f] !=-1){
            return dp[e][f];
        }
        
        int minVal = Integer.MAX_VALUE;
        
        for(int k = 1;k<=f;k++){
            
            // Check leftPart if exists else calculate
            int leftPart = dp[e-1][k-1], rightPart = dp[e][f-k];
            if(leftPart == -1){
                leftPart = superEggDrop(e-1,k-1);
                dp[e-1][k-1] = leftPart;
            }
            
            // Check leftPart if exists else calculate
            if(rightPart == -1){
                rightPart = superEggDrop(e,f-k);
                dp[e][f-k] = rightPart;
            }
            int tempVal = Math.max(leftPart, // Broken
                                   rightPart // Not broken
                                  );
            
            // int tempVal = Math.max(superEggDrop(e-1,k-1), // Broken
            //                        superEggDrop(e,f-k) // Not broken
            //                       );
            minVal = Math.min(tempVal,minVal);
        }
        return dp[e][f] = minVal + 1;
    }

5 DP on trees

Structure

Base condition
```
  if root ==null return 0;
```

Hypothesis

  int leftPath = helper(root.left);
  int rightPath = helper(root.right);

Induction

  int temp = _____;
  int ans = Max(temp,_____);

Return comparing temporary and final answer
```
  return max
```

5.1 Diameter of binary tree

Leetcode Diameter of Binary Tree
Keypoints the diameter does not need to pass through the root, it can pass from any node. So, need to know the max (left, right) from each node.

class Solution {
    int maxVal;
    public int diameterOfBinaryTree(TreeNode root) {
        maxVal = Integer.MIN_VALUE;
        int ans = helper(root);
        return maxVal;
    }
    
    int helper(TreeNode root){
        if(root == null){
            return 0;
        }
        int leftPath = helper(root.left);
        int rightPath = helper(root.right);
        //System.out.println(" Checking val : "+root.val +" l,r :"+leftNode+" , "+rightNode);

        maxVal = Math.max(maxVal, leftPath + rightPath);
        return Math.max(leftPath,rightPath) + 1;
    }
} 

5.2 Binary Tree Max Path Sum

The idea is, if the childs are -ve and the root is positive then take the root itself, instead of child. LeetCode Binary Tree Maximum Path Sum
Explanation ```java if( root == null) return 0; left = recurse(leftChild); right = recurse(rightChild);

// now find the max of all the four paths leftPath = root.value + left; rightPath = root.value + right; completePath = root.value + right + left;

result = max( root.value, leftPath, rightPath, completePath );

return max(root.value, leftPath, rightPath); ```

Pending topics and questions

MCM based
- 4.5 Min/Max value of expression
- 4.6 Balloon burst
- 4.7 Printing MCM
- 4.8 Scramble String
DP on trees
- 5.3 Binary Tree Max Path Sum
Fibonacci
Kadane’s algorithm
DP on grid

References

All credits to Youtuble playlist on DP by Aditya Verma. Above is just summarization and some additional references that I read and took some other references such as GeekForGeeks and LeetCode discussions.

Dynamic-Programming

Algorithms - My learning

Dynamic programming

1. Knapsack - 0|1

1.1 0-1 Knapsack

1.2 Subset Sum

1.3 Equal Sum

1.4 Count of Subset Sum

1.5 Min subset sum diff

1.6 Target Sum

1.7 No of subset given diff

2. Knapsack - Unbounded

2.1 Unbounded Knapsack

2.2 Rod Cutting

2.3 Coin Change I

2.4 Coin Change II

2.5 Maximum Ribbon Cut

3. LCS

3.1 Longest common Subsequence

3.2 Longest common Substring

3.3 Printing LC Subsequence and String

3.4 Shortest common supersequence

3.5 Min no of insertion and deletion a->b

3.6 Longest palindromic subsequence

3.7 Min no of deletions in string to make it palindrome

3.8 Longest Repeating subsequence

3.9 Sequence Pattern matching

3.10 Min no of insertions in string to make it palindrome

3.11 Note - TBD:

4. Matrix chain multiplication (MCM)

4.1 MCM base

4.2 Evaluate expression to TRUE/Boolean parenthization

4.3 Palindrome partitioning

4.4 Egg dropping problem

5 DP on trees

5.1 Diameter of binary tree

5.2 Binary Tree Max Path Sum

Pending topics and questions

MCM based

4.5 Min/Max value of expression

4.6 Balloon burst

4.7 Printing MCM

4.8 Scramble String

DP on trees

5.3 Binary Tree Max Path Sum

Fibonacci

Kadane’s algorithm

DP on grid

References

Next: Java-DS-Algo